Welcome to Sarthaks eConnect A unique platform where students can interact with teachers/experts/students to get solutions to1 The table of derivatives y = f(x) dy dx = f′(x) k, any constant 0 x 1 x2 2x x3 3x2 xn, any constant n nxn−1 ex ex ekx kekx lnx = log e x 1 x sinx cosx sinkx kcoskx cosx −sinx coskx −ksinkx tanx = sinx cosx sec2 x tankx ksec2 kx cosecx = 1 sinx −cosecxcot x secx = 1 cosx secxtanx cotx = cosx sinx −cosec2x sin− 1x √ 1−x2 cosP 3=2)we get dy dx = 2x 8y = 2(1) 8(p 3=2) = 1 2 3 So the equation of the tangent line is (y p 3=2) = 1 2 p

Ma 136 Review T 3
Tan 2x differentiation
Tan 2x differentiation-Find the derivatives of the following functions f (x) =xe2x g(t) = p t(tbt) h(x) =3 x(a p xb)(2x1= p x) Professor Christopher Hoffman Math 124 We break the functionf(x) =xe2xup into two partsxande2x Then we take the derivatives of the two partsThe derivative of tan x, sec x & tan x – The derivative of a function of a real variable measures the sensitivity to change of the function value (output value) with respect to a change in its argument (input value) Derivatives are a fundamental tool of calculus For example, the derivative of the position of a moving object with respect to time is the object's velocity this measures how
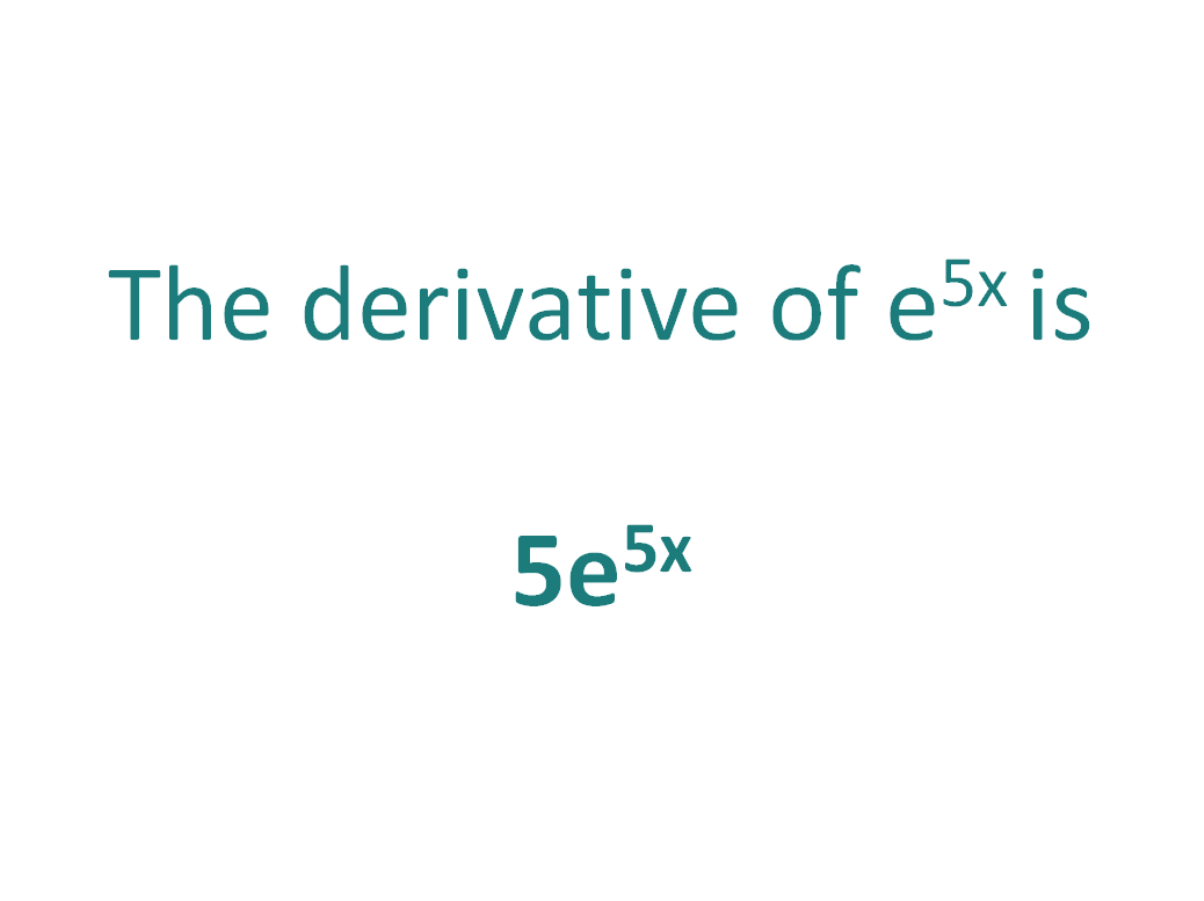



The Derivative Of E 5x Derivativeit
The derivative of tan x is sec 2x However, there may be more to finding derivatives of tangent In the general case, tan x is the tangent of a function of x, such as tan g (x) Note in the simpleAs there is no way to immediately integrate tan^2 (x) using well known trigonometric integrals and derivatives, it seems like a good idea would be writing tan^2 (x) as sec^2 (x) 1 Now, we can recognise sec^2 (x) as the derivative of tan (x) (you can prove this using the quotient rule and the identity sin^2 (x) cos^2 (x) = 1), while we getDifferentiate wrtx du/dx = 2/ (1 x 2) Let v = sin 1 2x/ (1x 2) Put x = tan θ So v = sin 1 2 tan θ/ (1 tan 2 θ) = sin 1 sin 2θ = 2θ = 2 tan 1 x dv/dx = 2/ (1 x 2)
Get RS Aggarwal Solutions for Class 12 Chapter Differentiation here BeTrainedin has solved each questions of RS Aggarwal very thoroughly to help the students in solving any question from the book with a team of well experianced subject matter experts Practice Differentiation questions and become a master of concepts All solutions are explained using stepbystep approachSolution First we differentiate as the product of two functions y′(x) = (sinnxcosnx)′ = (sinnx)′ cosnxsinnx(cosnx)′ Next, using the power rule and the chain rule, we have y′(x) = nsinn−1x⋅ (sinx)′ ⋅cosnxsinnx(−sinnx)⋅ (nx)′ = nsinn−1xcosxcosnx−nsinnxsinnx = nsinn−1x⋅ (cosxcosnx− sinxsinnx) Apply now theExample 16 Calculate the derivative of the function \y = \left( {2 – {x^2}} \right)\cos x 2x\sin x\ at \(x = \pi\)
Differentiate the following from first principle tan 2x > 11th > Maths > Limits and Derivatives > Derivative of Trigonometric Functions > Differentiate the followingThe process of calculating a derivative is called differentiation Follow the rules mentioned in the above derivative calculator and understand the concept for deriving the given function to differentiate Make use of this free online derivative calculator to differentiate a functionUse implicit differentiation to finddy dx if 4y2x2=4 Find the tangent line at the point at(1 p 3=2) 4y2x2 = 4 d dx 4y 2x = d dx (4) 8y dy dx 2x = 0 dy dx = 2x 8y dy dx = x 4y Professor Christopher Hoffman Math 124 At the point(1;



2



2
J Josephine New member Joined Messages 12 #1 Differentiate with respect to x ln tan 2x The answer is 4 cosec 4x So, I've gotten dy/dx = 2 sec^2 2x/tanDifferentiate the sec^1 ((1 tan^2x)/(1 tan^2x)) wrt x asked in Differentiation by Subnam01 (5k points) differentiation; So far, we have learned how to differentiate a variety of functions, including trigonometric, inverse, and implicit functions In this section, we explore derivatives of exponential and logarithmic functions



How To Differentiate A 2x In Fact What Is The General Rule For Functions Like A Kx Where K Is Any Constant Quora




Sorry For This Question But Is Tan 2x 3 The Same With Tan 2x 3 Or No Because My Classmates Differentiated This By Changing Tan 2x 3 To Tan 2x 3 Because I Don T Know Any
Differentiation of ln tan 2x with respect to x Thread starter Josephine; Example 22 Find the derivative of tan (2x 3) Let y = tan (2x 3) We need to find derivative of y, ie 𝑑𝑦/𝑑𝑥 = (𝑑 tan〖(2𝑥3)〗)/𝑑𝑥 = sec2(2x 3) × (𝑑(2𝑥 3))/𝑑𝑥 = sec2 (2x 3) × 2 = 2 sec2 (2x 3) (As (tan x)' = sec2 x) Show More #"note "tan^2x=(tanx)^2# #"differentiate using the "color(blue)"chain rule"# #"given "y=f(g(x))" then"# #dy/dx=f'(g(x))xxg'(x)larr" chain rule"# #"y=(tanx)^2#



2




Examples Int Tan 2x Sec 4x Dx
By using the quotient rule and trigonometric identities, we can obtain the following derivatives `(d(csc x))/(dx)=csc x cot x` `(d(sec x))/(dx)=sec x tan x` `(d(cot x))/(dx)=csc^2 x` In words, we would say The derivative of `csc x` is `csc x cot x`, The derivative of `sec x` is `sec x tan x` and The derivative of `cot x` is `csc^2 x`, Explore animations of these functions with Use logarithmic differentiation to find this derivative \(\ln y=\ln (2x^41)^{\tan x}\) Step 1 Take the natural logarithm of both sides \(\ln y=\tan x\ln (2x^41)\) Step 2 Expand using properties of logarithmsIf the derivative of a is b, then the integral of b is a C, where C is a constant This tells us that to check our work, we can take the integral of 2sec 2 x tan x, and we should get sec 2 x



2




Differentiate Tan Root 2x Maths Continuity And Differentiability Meritnation Com
The differentiation of trigonometric functions is the mathematical process of finding the derivative of a trigonometric function, or its rate of change with respect to a variableFor example, the derivative of the sine function is written sin′(a) = cos(a), meaning that the rate of change of sin(x) at a particular angle x = a is given by the cosine of that angleDifferentiation Exercise 10J page 449 1 Find the second derivative of (i) x11 (ii) 5x (iii) tan x (iv) cos 1 x Solution 2 Find the second derivative of (i) x sin x (ii) e 2x cos 3x (iii) x3 logxDifferentiating tan2x should give 2sec (2x)^2 Such type of differentiation is explained in C3 The general way of differentiating such an expression, tan (y), is to differentiate the part in bracket and multiply it with sec (y)^2 Your expression is tan (2x)




Derivative Of Tan 2x 3 From First Principle Brainly In




Rd Sharma Solutions For Class 11 Maths Updated 21 22 Chapter 30 Derivatives Download Free Pdf
`y = sqrt(x) e^(x^2 x) (x 1)^(2/3)` Use logarithmic differentiation to find the derivative of the function 3 Educator answers eNotescom will help you with any book or The derivative of sin x is cos x, The derivative of cos x is −sin x (note the negative sign!) and The derivative of tan x is sec 2x Now, if u = f(x) is a function of x, then by using the chain rule, we haveDifferentiate the following wrt x tan1\(\left(\cfrac{32\text x}{16\text x}\right)\) tan1(3 2x)/(1 6x)




How Do You Differentiate F X Tan 3x 2 E 1 X 1 Using The Quotient Rule Socratic




Differentiate The Following W R T X Sin 1 1 Tan 2x1 Tan 2x
Since 2 2 is constant with respect to x x, the derivative of 2 x 2 x with respect to x x is 2 d d x x 2 d d x x Move 2 2 to the left of e tan ( 2 x) sec 2 ( 2 x) e tan ( 2 x) sec 2 ( 2 x) Differentiate using the Power Rule which states that d d x x n d d x x n is n x n − 1 n x n 1 where n = 1 n = 1Click here👆to get an answer to your question ️ Differentiate sin^2 3x tan^3 2x Join / Login > 11th > Applied Mathematics > Differentiation > Rules of differentiation = 6 sin 2 3 x tan 2 2 x sec 2 2 x 6 sin 3 x cos 3 x tan 3 2 xThe graphs of \( \tan(x) \) and its derivative are shown below Derivative of the Composite Function tan (u(x)) We now have a composite function which is a function (tan) of another function (u)




Y E X Log Tan 2x Find Dy Dx Brainly In
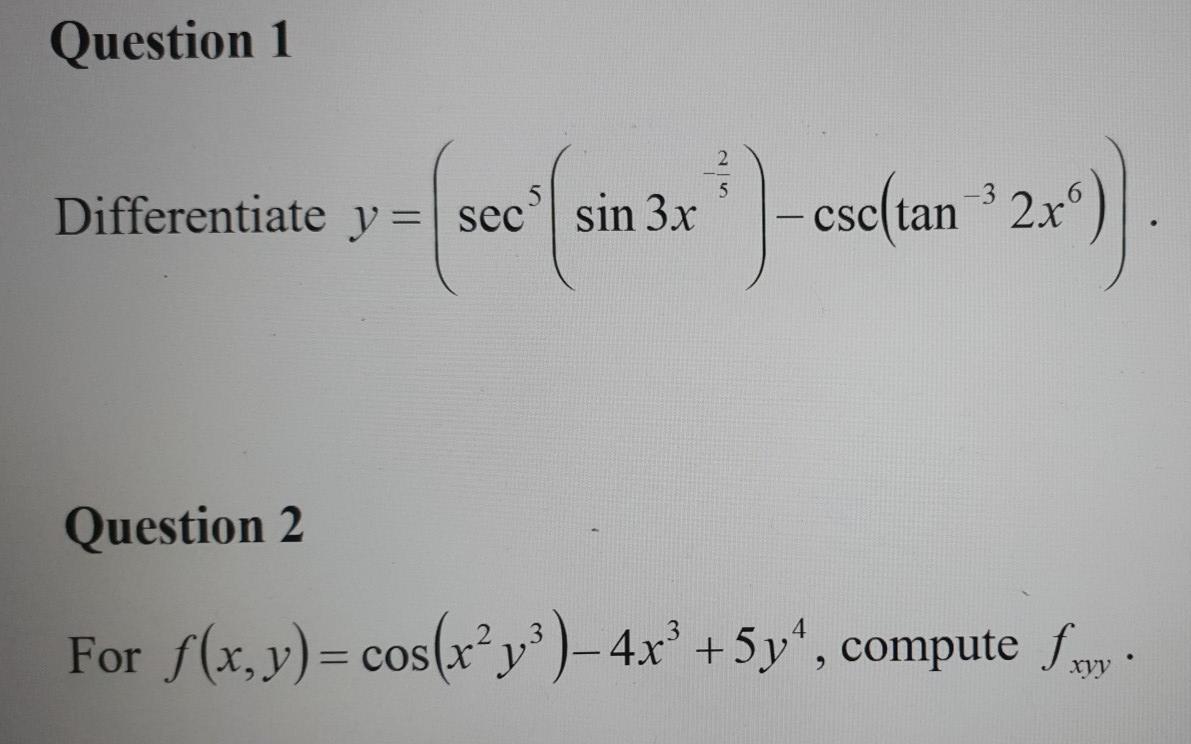



Question 1 5 Differentiate Y Secsin 3x Csc Tan 2x Chegg Com
We can use the chain rule to find the derivative of 3sec 2 (3x) (bearing in mind that the derivative of sec^2(x) is 2sec 2 (x)tan(x)) and it gives us a result of 18sec 2 (3x)tan(3x) The second derivative of tan(2x) is 18sec 2 (3x)tan(3x) $\frac13\tan^3x\tan xx$ I solved it and got $\frac13\cdot3\tan x\sec^2x1$ by using chain rule I got $\tan x\tan^3x\tan^2x$ The answer is $\tan^4x$ I am not able to get thisDerivative of the Tangent Squared Function In this tutorial we shall discuss the derivative of the tangent squared function and its related examples It can be proved by the definition of differentiation We have a function of the form y = f ( x) = tan 2 x By the definition of differentiation we have d y d x = lim Δ x → 0



Http People Whitman Edu Hundledr Courses M125f05 Examrev2sol Pdf



1
Hence, evaluating the derivative of the function using the quotient rule yields `f'(x) = ( 2tan x/(cos^2 x))/((1 tan x)^2)` Approved by eNotes Editorial Team We'll help your grades soarFormer SDE at Bharat Sanchar Nigam Limited (BSNL) · Let y = 5cosx 4 (1tan^2x)= 5cosx 4sec^2x , differentiating both side wrt x & applying chain rule when reqd dy/dx = 5 (sinx) 4*2 secx d/dx (secx) => dy /dx = 5sinx 8secx *secxtanx => dy/dx = 5sinxDifferentiate tan^(1)(sqrt(√(1x^2)/x) with respect to cos^(1)(2x√(1x^2)) ,when x!=0 CBSE CBSE (Arts) Class 12 Question Papers 17 Textbook Solutions Important Solutions 24 Question Bank Solutions Concept Notes & Videos 531 Time Tables 18




Logarithmic Differentiation Utrgv



Http Math Hws Edu Mitchell Math130f16 Practest2 Pdf
The function you are differentiating is Take x, calulate tangent, then square and last calculate logarithm You must begin by the end, that is, you must differentiate the logarithm first y ′ = (tan2x) ′ tan2x Now differentiate the square y ′ = 2tanx(tanx) ′ tan2xDifferentiation of Trigonometric Functions The following table contains examples of differentiated trigonometric functions Worked examples of many of those you see in this table are provided at the bottom of this page y = Sin (x) dy/dx = Cos (x) Same goes for cos and tan Note Don't confuse sin1 x with (sin x)1 They are different Writing sin1 x is a way to write inverse sine whereas (sin x)1 means 1/sin x Implicit Differentiation Implicit differentiation is a method that makes use of the chain rule to differentiate implicitly defined functions




Ex 7 2 21 Integrate Tan2 2x 3 Class 12 Cbse Ex 7 2



Activity 4 Determine The Antiderivatives Of The F Gauthmath
The Second Derivative Of tan^2x To calculate the second derivative of a function, differentiate the first derivative From above, we found that the first derivative of tan^2x = 2tan (x)sec 2 (x) So to find the second derivative of tan^2x, we need to differentiate 2tan (x)sec 2 (x)Let, u = (tanx)^2 and v = (cosx)^2 Now differentiating u and v with respect to x Then du/dx = 2 tanx (secx)^2 And dv/dx = 2 cosx (sinx)Derivatives Derivative Applications Limits Integrals Integral Applications Integral Approximation Series ODE Multivariable Calculus Laplace Transform Taylor (tan^{2}x\right) en Related Symbolab blog posts High School Math Solutions – Derivative Calculator, the Chain Rule In the previous posts we covered the basic derivative rules




Y 3 Log 9 1 Tan 2 X Then Dy Dx



Www Math Purdue Edu Kyochman Ma Lesson14 Notes Implicitdifferentiation Pdf
SolutionShow Solution Let Let y = sin 2 ( 2 x 1) Differentiate it with respect to x we get Differentiate it with respect to x we get , d y d x = d d x sin 2 ( 2 x 1) using chain rule = 2 sinPractice Derivatives of tan(x), cot(x), sec(x), and csc(x) Worked example Derivative of sec(3π/2x) using the chain rule Practice Differentiate trigonometric functions Derivative of tan(x) (old) This is the currently selected item Differentiating trigonometric functions review= 2 tan x tan 2 x tan 3 x tan 4 x × cosec 2x 2 cosec 4x 3 cosec 6x 4 cosec 8x



2




1 Use The Four Step Process To Find The Derivative Chegg Com
Differentiation of tan x The function y=tan x can be differentiated easily Since tan x = sin x / cos x, we can replace the trigonometry identity with this Since we have a function divided by a function we can use the quotient rule, and the top part of the fraction becomes f (x) = sin x, and the derivative of sin x is cos x find the derivative using implicit differentiation tan(x − y) = y/(5 x^2) please add explanation i get stuck when trying to bring dy/dx to one side of the equationFree implicit derivative calculator implicit differentiation solver stepbystep This website uses cookies to ensure you get the best experience By using this



Http Neumann Math Unideb Hu Muzsnay Pdf 0606en 2 Differentiation 3 Pdf




Powers Of Trigonometric Functions




Ppt Introduction To Implicit Differentiation Powerpoint Presentation Id




Integral Of Tan 2x Cot 2x 2 Calculus 1 Trig Integrals Calculus Mathematics Email Subject Lines




05 Derivative Of Tangent Function Tan2x And Tanx 2 Youtube




Ppt Download




Answered 1 Differentiate F X E Tan 2x X Bartleby




Prove That Derivative Of Tan X Is Sec 2 X By First Principle



2



Tan 2x Tan 2x




Derivative Of Inverse Tangent Video Khan Academy




Ma 136 Review T 3




Differentiate The Following W R T X Tan 1 E 2x 1e 2x 1




Differentiate Tan 1 2x 1 X 2 With Respect To Sin 1x 2x 1 X 2 Brainly In




Find The Derivative From First Principle Of Function




Differentiate X 2 Tan X




Differentiation Of Tan 2 X And X 3 X 4 Youtube



1




Derivative Of Sec 3 2x




06 Derivative By Substitution Of Trigonometric Ratio Tan 2 X 3 2tans Tan2x Youtube



Www Mathsdiy Com Differentiation Solutions




Differentiate Tanx Tan 2x Tan 3x Tan 4x W R T X Youtube
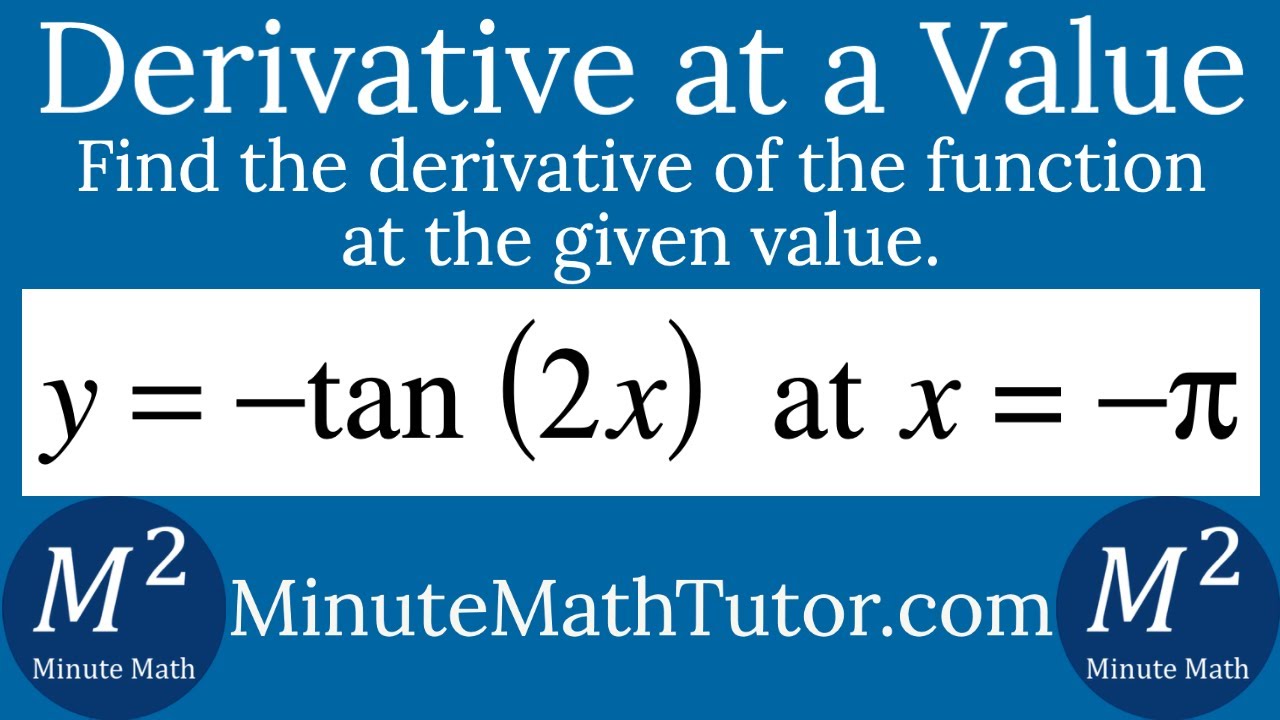



Find The Derivative Of Y Tan 2x At X P




Derivative Of F X 2x 2ln 2x With Product And Chain Rule Chain Rule Math Videos Derivative




Differentiate The Following From First Principle Tan2x Youtube



2
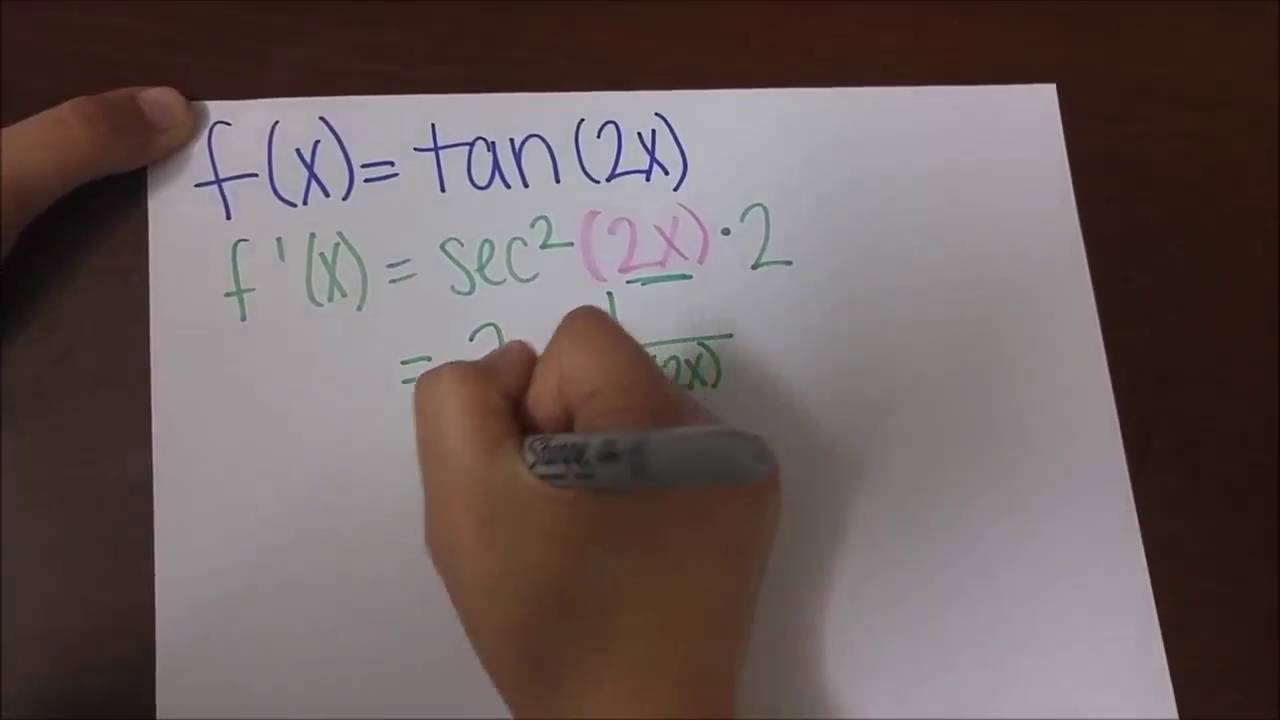



Ii F Find Derivative Of Tan 2x At X Pi 6 Youtube




Ex 13 1 22 Lim X Pi 2 Tan 2x X Pi 2 Chapter 13 Class 11



Http Www Sequoiahs Org Documents 1seqfix Ibmathhl Pdf



Solved K U 1 Differentiate The Following Choose 4 Only Marks A Y Tan 2x 1 Cot 2x B F X Xsin X 1 X C G X Sec Quot 6x Cos Course Hero




Second Derivative Of Tan 2x Youtube




If Y 2 Tan X 2 Prove That Dy Dx 2 1 Cosx Maths Application Of Derivatives Meritnation Com




Answered 1 Find The Derivative Of The Function Bartleby




Differentiate The Following From First Principle Tan 2x




If Y Sqrt 1 Tan 2x 1 Tan 2x Then Dy Dx
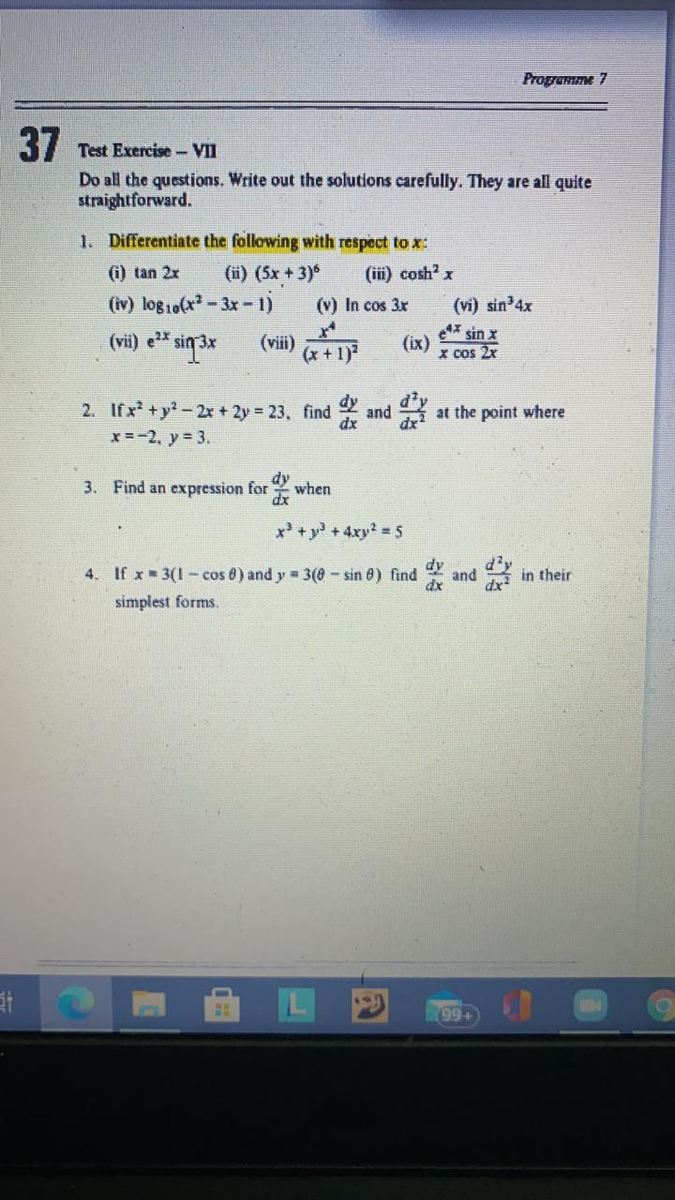



Answered Straightforward 1 Differentiate The Bartleby




Rd Sharma Solutions For Class 11 Maths Updated 21 22 Chapter 30 Derivatives Download Free Pdf




Resonance Aieee Iit Study Material Maths Complete Pdf By S Dharmaraj Issuu




Differentiation Of Tanx 2 Youtube




What Is The Derivative Of Tanh X Quora Felix Lucas En Ligne Catalogue Pdf



What Is The Derivative Of Tan 1 Sec X Tan X Quora



2



Http Www Pstcc Edu Facstaff Jwlamb 1910 3 8problems Pdf




Find The Derivative Of The Following Functions 1 Gauthmath
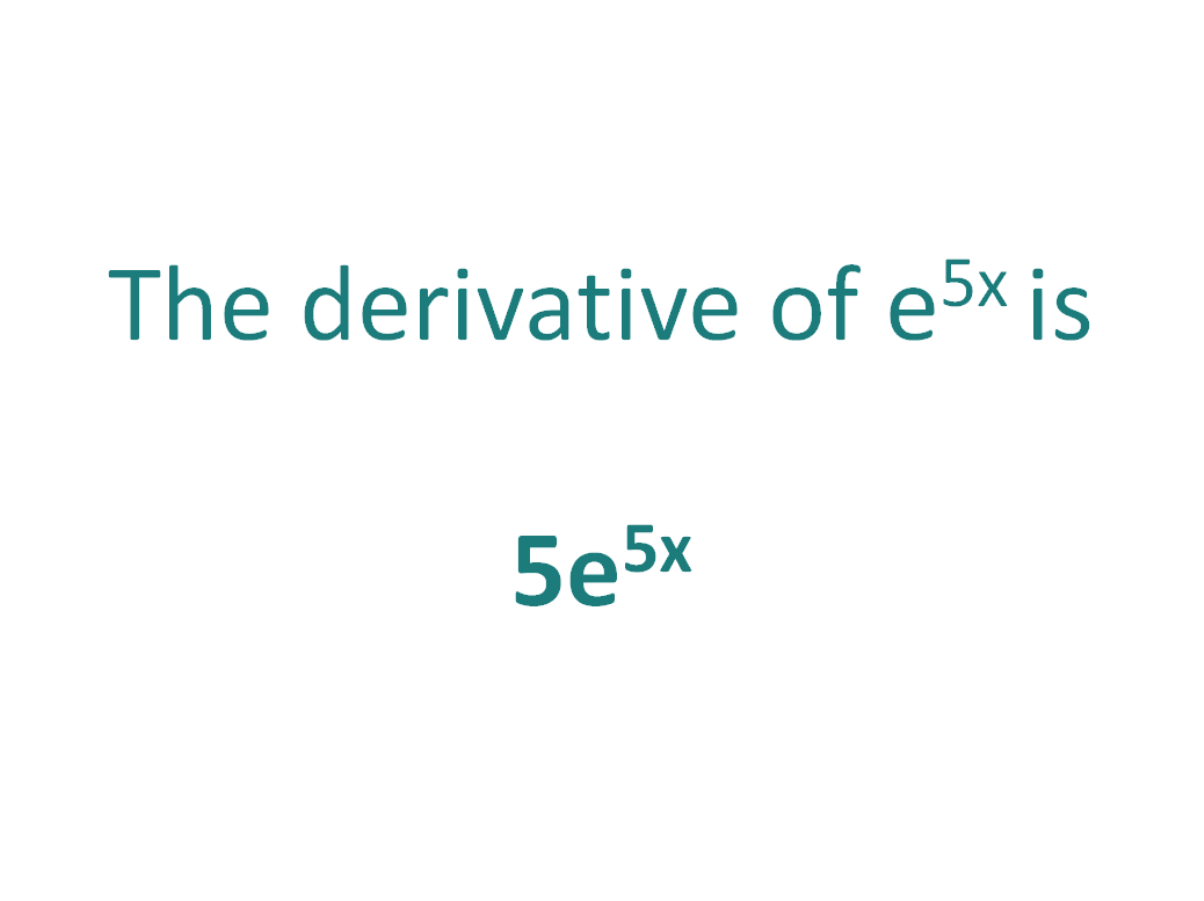



The Derivative Of E 5x Derivativeit




9 If G 3 4 G 3 5 F 3 9 And F 8 Find H 3 Chegg Com



Http Www Math Pitt Edu Athanas Math 02 Calculus I Practicederivatives Pdf




Differentiate Tan 2 2x 1 With Respect To Log 2x 1 Maths Continuity And Differentiability Meritnation Com




Derivatives Of Trigonometric Functions Ppt Download



1




Ddx Tan 22x Tan 2x1 Tan 22xtan 2x Cot3x



2



2




Differentiate The Following From First Principle Tan 2x 1



Web Auburn Edu Holmerr 1617 Textbook Derivsummary Print Pdf




Example 22 Find Derivative Of Tan 2x 3 Chapter 5 Class 12




Find The Derivative Of The Given Function Y Tan 2x 1 Cot 2x I Tried Converting The Original Function In Terms Of Sin And Cos But It Was Still Too Complicated To Be Called Simplified
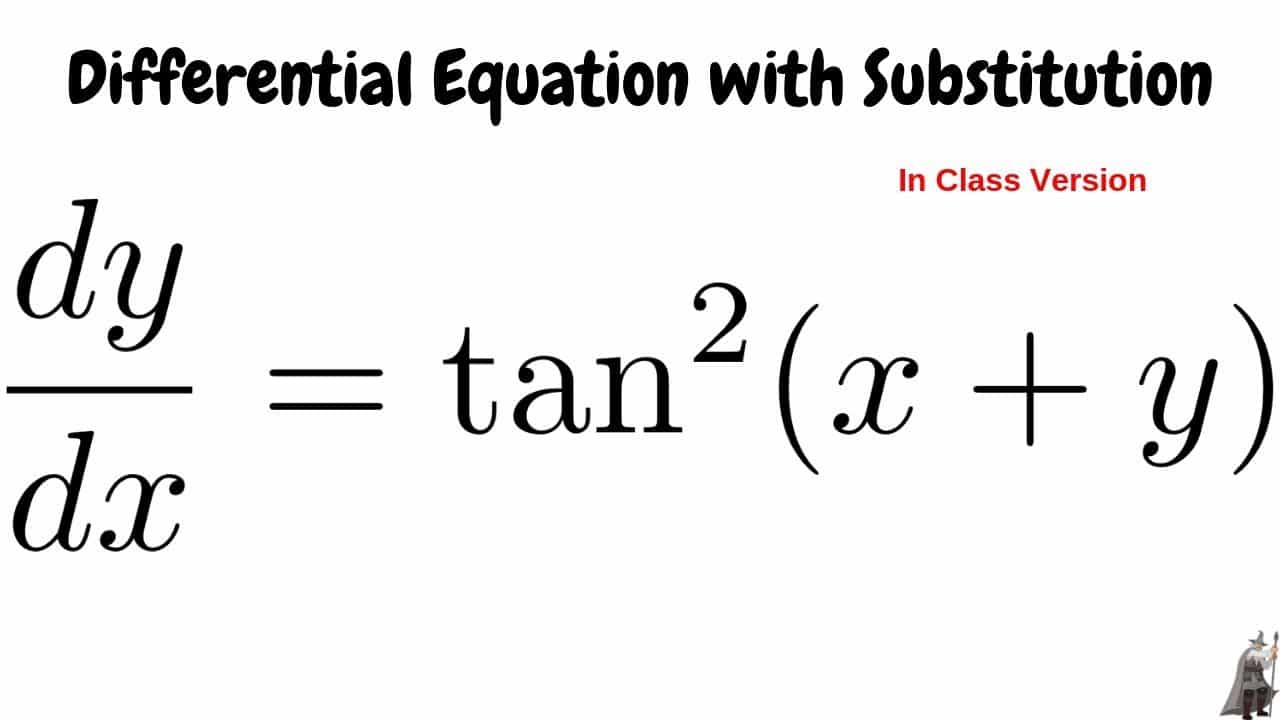



Derivative Of Tangent X Sec X Tan X Longer Free Tutorial Get Education Bee



Http Neumann Math Unideb Hu Muzsnay Pdf 0606en 2 Differentiation 3 Pdf
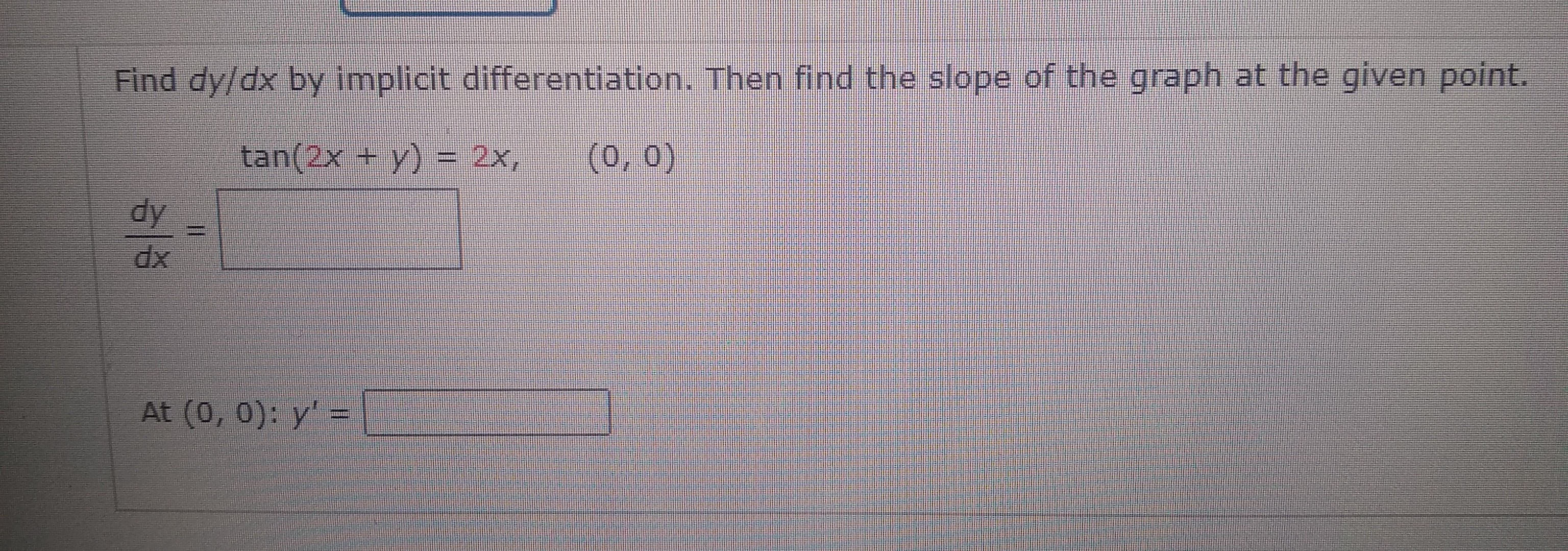



Answered Find Dy Dx By Implicit Differentiation Bartleby




How Do You Differentiate Y Sin X 6 Tan X 2 X 2 2 2 Socratic




Derivative Rules For Trigonometric Functions




Show That Z Ln X 2 Y 2 2 Tan 1 Y X Satisfies The Laplaces S Equation Mathematics Stack Exchange



Mryangteacher Weebly Com Uploads 7 7 0 2 Ab Fall Review Packet 3 Solutions Pdf




Derivative Of Tan X Old Video Khan Academy
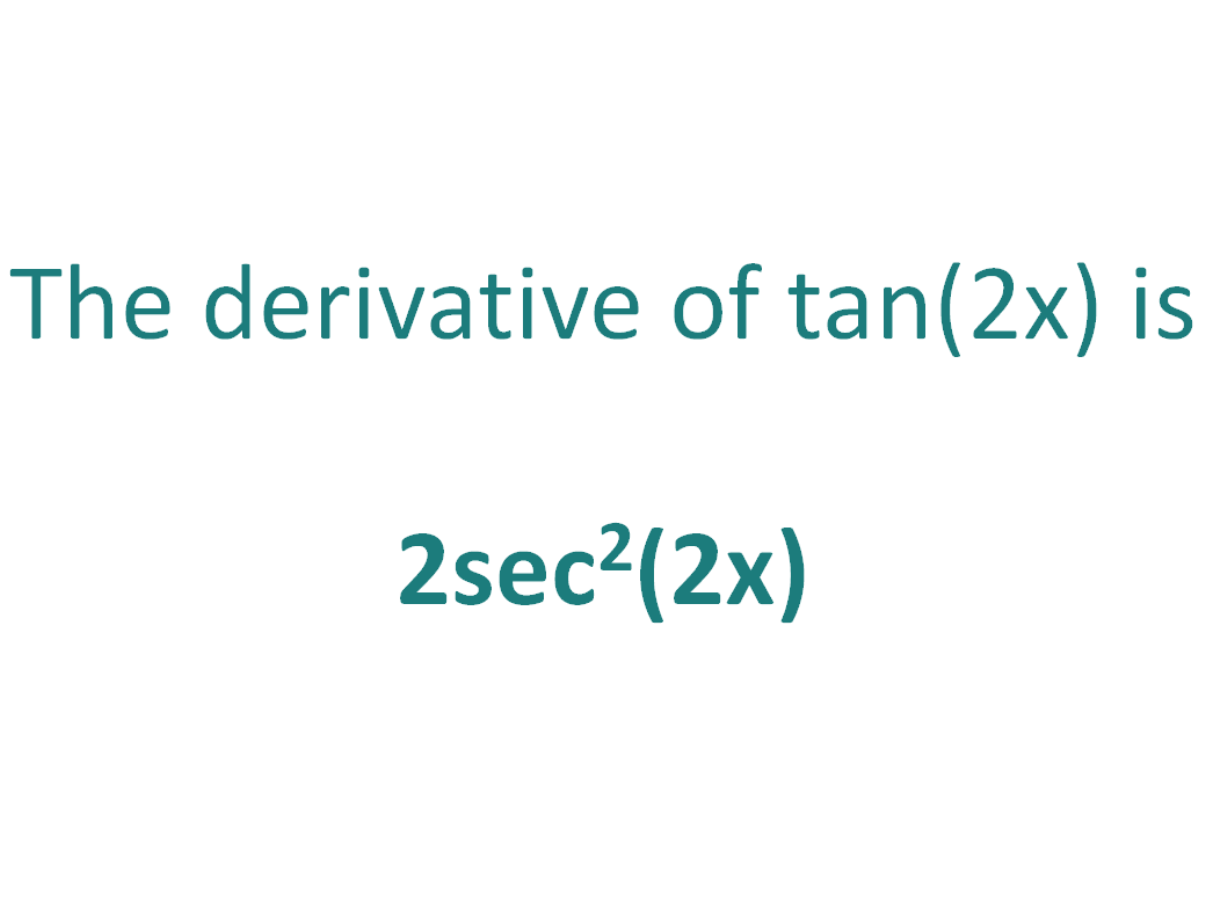



The Derivative Of Tan 2x Derivativeit



2



2



Www Mvcc Edu Learning Commons Pdf Sp Ma151finalexamreview Pdf




Differentiate Tan 1 2x 3 By Any Method Maths Continuity And Differentiability Meritnation Com




Tan2 Derivative ただの悪魔の画像




Solved Find The Derivative Of The Trigonometric Function Chegg Com



Www Math Purdue Edu Kyochman Ma Lesson14 Notes Implicitdifferentiation Pdf




Misc 44 Value Fo Tan 1 2x 1 1 X X2 Dx Is Miscellaneous



Solved Activity Exercise No 9 Differentiation Of Trigonometric Functions Find Y Of The Following Function Dx 1 Y Sin2 2x Cos 4x 2 Y Sec2 Course Hero



Www Math Purdue Edu Kyochman Ma Lesson14 Notes Implicitdifferentiation Pdf



Qualifications Pearson Com Content Dam Pdf Subject Updates Mathematics Detail Of Amendments Pdf



2
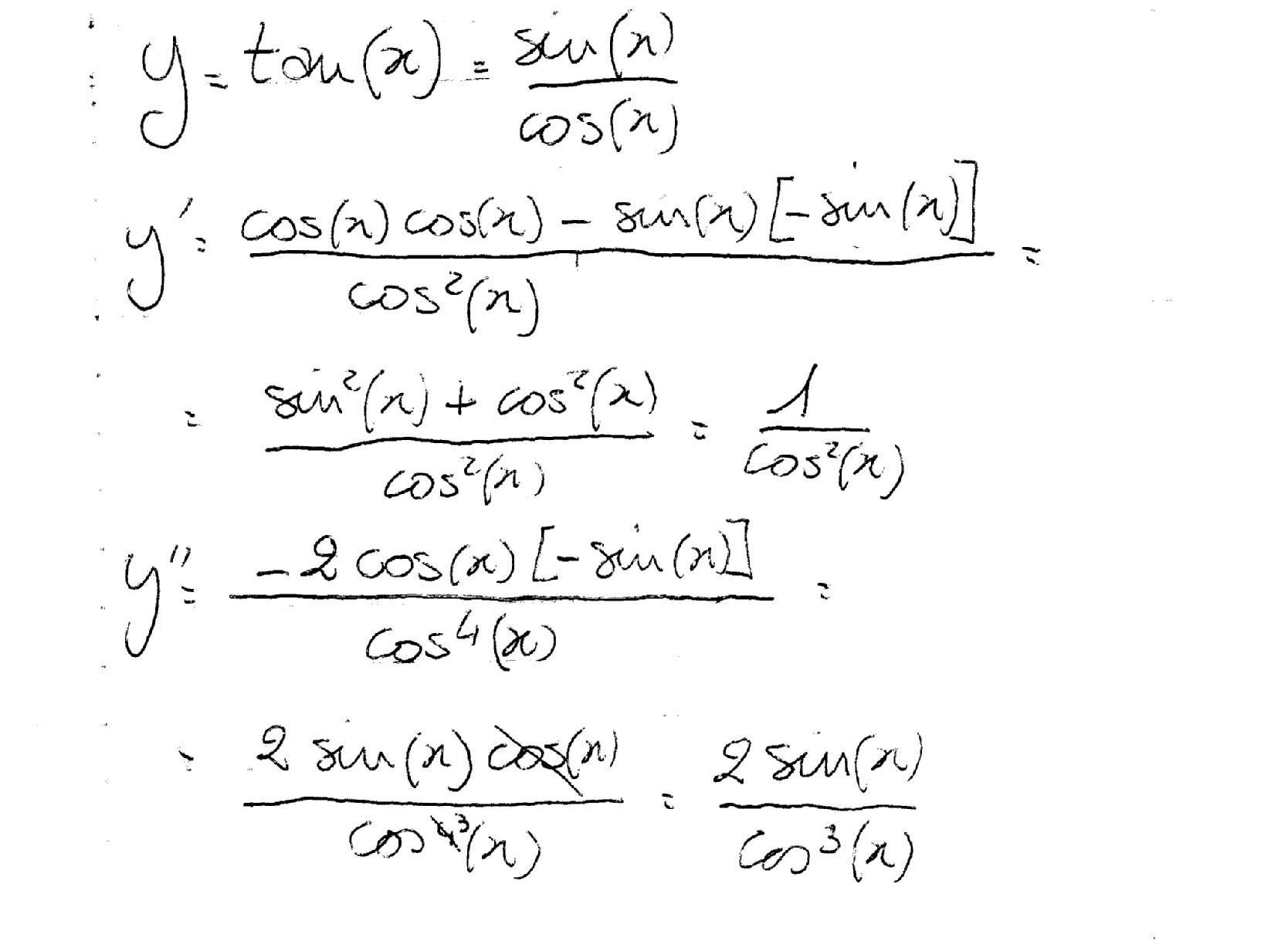



What Is The 2nd Derivative Of Y Tanx Socratic



1



0 件のコメント:
コメントを投稿